Problem 🤔

Say you have an array for which the i-th element is the price of a given stock on day i.

You were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock).

Design an algorithm to find the maximum profit.

Note

• You cannot sell a stock before you buy one.

Example 1

Input: [7,1,5,3,6,4]

Output: 5

Explanation

Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Not 7-1 = 6, as selling price needs to be larger than buying price.

Example 2

Input: [7,6,4,3,1]

Output: 0

Explanation

In this case, no transaction is done, i.e. max profit = 0.

Real World Applications 🌎

We all want to get rich selling stocks right? Seriously now, think of the problem this way. Given a time series where each index represents time and each value is a price, find the maximum “positive” difference in the time series. This sounds more generic already and can be applied for multiple use cases.

The Finer Details 🔎

Our first naive approach would be to consider every day as the “buy” day and see what the maximum money we could make would be. Let’s give this a look.

Solution 💡 - Brute Force

Complexity Analysis 🧮

Time complexity

O(n^2)

Loop over input with nested for loops.

Space complexity

O(1)

Constant amount of auxillary variables used.

Solution 💡 - Optimal

This works! But can we do better?

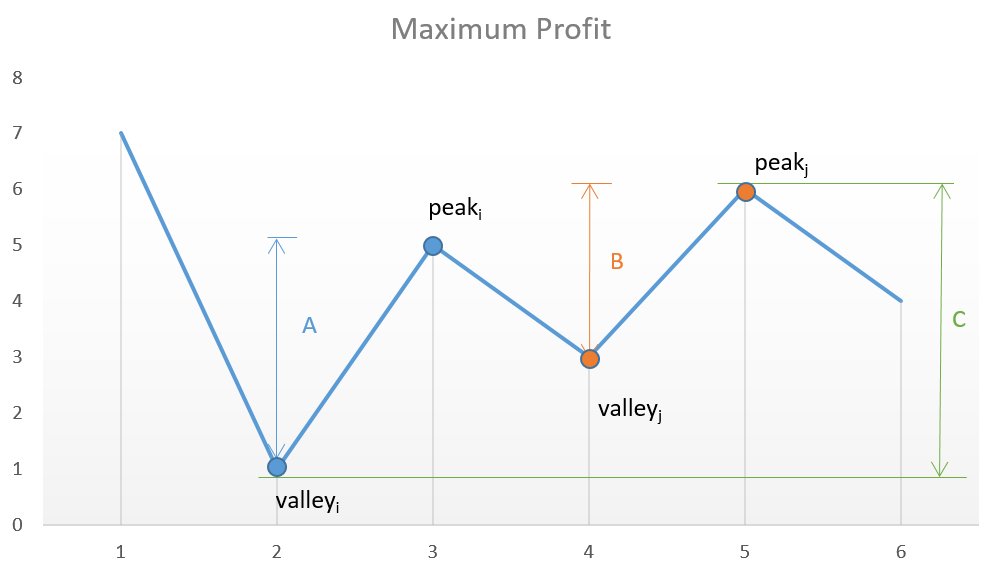
Let’s examine whether we really need two nested for loops. To find the maximum difference we’ll want to find the lowest priced day such that it’s subsequent highest price day creates the biggest difference. Everytime we find a new “all time low” we can save it and hope for a better “all time high”!

Complexity Analysis 🧮

Time complexity

O(n)

Loop over input once

Space complexity

O(1)

Constant amount of auxillary variables used.

Takeaways 🎉🥳

When the input of a problem is seemingly simple it can be tempting to go for a naive solution. The trick here is to stop and think about which conditions will give us a max profit. Take your time here and don’t rush! Once we’re clear on this the implementation is relatively easy!

Resources 📚 💻

Leetcode