Problem 🤔

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8

Output: 6

Explanation

The LCA of nodes 2 and 8 is 6.

Example 2

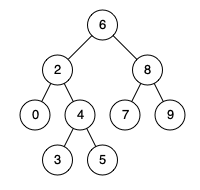
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4

Output: 2

Explanation

The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3

Input: root = [2,1], p = 2, q = 1

Output: 2

Constraints

• All nodes are unique
• p != q
• p and q will exist in the BST

Real World Applications 🌎

Looking at a family tree? This is a super helpful function for any data representation that has a lineage!

Recursive Solution 💡

As we’ve seen for countless other tree problems, a recurisve solution often lets us write elegant and concise code, especially when dealing with traversals. Let us start off with this approach.

1) If the root is either p or q, since we are promised that both nodes are present we know that the other node is definitley in the subtree! We can call it a day.

2) How do we recurse the rest of the tree? Let’s think about what our recursion should do. A helpful recursive function would return the null if p and q are not in the tree. Otherwise, it can return a pointer to our node :) We can run this check on our left and right subtrees respectively.

Complexity Analysis 🧮

Time Complexity

Run time: O(n)

Traverse all nodes in the tree once.

Space Complexity

O(n)

Unbalanced bst will require recursing on every node. A height balanced bst will require O(log(n)).

The Finer Details 🔎

Let’s define a divergent point as the first node in the tree where there is a split and p and q belong to different subtrees. We want to traverse down the tree to the earliest divergent point. We can use the fact that bst is … sorted and do this efficiently!

Optimal Solution - Iteratively 💡

Complexity Analysis 🧮

Time Complexity

Run time: O(n)

Visit every node in the tree once, worst case.

Space Complexity

O(1)

Only constant helper variables declared.

Takeaways 🎉🥳

• Break down the recursion into smaller digestible steps, before concerning yourself with implementation details.
• Lowest common ancestor problems will always look for the divergent point! This is a key insight, and makes the iterative version easier to understand.

Resources 📚

Leetcode

• Cracking the Coding Interview, 4.8 First Common Ancetor (Note, here we have a BST and not binary tree)