Problem 🤔

Given an integer n, return the number of structurally unique BST’s (binary search trees) which has exactly n nodes of unique values from {1,..,n}.

Example 1

Input: n = 3

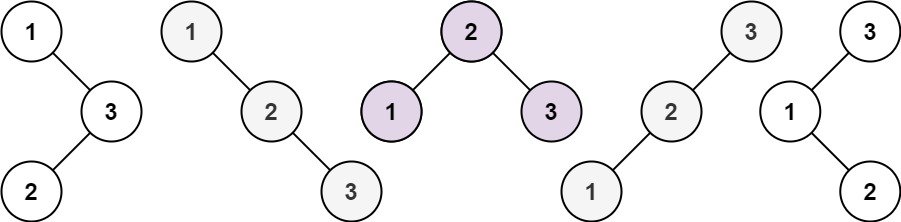
Output: 5

Example 2

Input: n = 2

Output: 2

Example 3

Input: n = 1

Output: 1

Example 4

Input: n = 0

Output: 1 (empty tree)

Real World Applications 🌎

I’ve never been asked to calculate the amount of unique binary search trees given an n. If you can find a strong parallel for this in real life, lmk in the comments :)

The Finer Details 🔎

There are sooo many ways we can look at this. For me, the most intuitive is to ask how many uniqe sub trees can I create given a certain root. For every root, we can ask ourselves:

For root i, how many right subtrees can I create with k nodes? How many left subtrees can I create with j nodes? Our constraint here is that n = k + j + 1, because our unique sub tree has a question constraint of using all the values {1,..,n}.

Again, here we want to be efficient and cache our computations. Similarly to the coin change problem, let’s be clear about what our dp cache should actually hold!

dp[i] can represent the amount of unique subtrees we can create with i values. Perfect! Our final computation for a given n can simply be the trees we can create with k nodes in the right subtree and j nodes in the left subtree.

For example, we can calculate n = 3 by simply computing the following:

• amount of trees with 0 nodes in left subtree, 2 nodes in the right subtree
• amount of trees with 1 nodes in left subtree, 1 nodes in the right subtree
• amount of trees with 2 nodes in left subtree, 0 nodes in the right subtree

Of course, our base case of n = 1 and n = 0 is 1, because with one node we can return only one tree and with no nodes we can return an empty tree. Let’s put this into code!

Solution 💡

Complexity Analysis 🧮

Time Complexity

O(n^2)

Nest for loops — worst case each is of size n.

Space Complexity

O(n)

Our dp cache is of size n!

Resources 📚

Leetcode